Natural Fecundity/Fertility
Model Inputs \(\rightarrow\) Biological Parameters \(\rightarrow\) Natural Fecundity/Fertility
Overview
Fecundity is defined as the biological capacity to reproduce, a theoretical potential that differs from fertility, which is the actual realization of a live birth. Fecundity is therefore more difficult to measure, but has been estimated by examining populations which do not use deliberate family planning - so called “natural fertility” populations that likely reflect natural age-related physiological changes in reproductive capacity and natural sterility.[1,2]
Natural fertility
Natural fertility was first estimated by Henry 1961,[3] based on empirical data from 13 populations of married women who did not use deliberate birth control. While the absolute level of fertility varied among populations, it was observed that relative fertility rates followed the same characteristic age profile. In later work, Coale and Trussell[4,5] averaged 10 of these 13 natural fertility populations to obtain more refined estimates after discarding those suspected to be biased by age misreporting. More recent analyses have focused on fitting statistical models to the empirical data.[1,6,7,8]
Age patterns of natural fertility may vary somewhat between populations, with patterns determined by context-specific reproductive behaviors.[1] However, after adjusting each population to the same fertility rate at age 20, the age-related decline in fertility is almost identical in all populations, suggesting a common pattern of female reproductive aging.[2] Evidence also suggests that even very different marriage patterns have only a minor effect on the overall fertility pattern.[1]
Natural fecundity
However, note that “natural fertility” is based on observed live births, and therefore underestimates total pregnancies since it does not take into account pregnancy loss (e.g. spontaneous or elective abortion). Since the model does simulate the risk of pregnancy loss, we need to estimate the probability of natural fecundity (i.e. risk of conception), rather than natural fertility. This estimation is complicated by the fact that risk of miscarriage varies substantially by maternal age. To address the inherent uncertainty in this parameter we fit quadratic splines to estimated rates of pregnancy after adjusting for age-specific risks of miscarriage.
Data
For baseline natural fertility estimates, we averaged age group data from Coale and Trussell[4] and Xie[6] - estimates were similar from both sources. This provided the relative shape of fertility by age. To adjust for pregnancy loss, we used estimates of miscarriage from Andersen 2000.[9] We further inflated the priors by 25% to better approximate other data from Trussell 2007,[10] which estimated that women not using contraception faced an annual probability of pregnancy of 0.85. However, the population of women under study was desiring pregnancy, and the denominator also only included women at risk of pregnancy (i.e. not already pregnant or breastfeeding). Thus we would expect the actual probability to be lower in the general population.
Parameters
We fit quadratic B-splines to the midpoints of the natural fecundity age groups. Spline Width: 30
| Spline # | Knot Location | Height |
|---|---|---|
| 1 | 20 | 0.66 |
| 2 | 30 | 0.58 |
| 3 | 40 | 0.5 |
We used a hierarchical model with 4 levels (global/area/region/country) to account for potential differences in factors that affect fecundity (e.g. biological and cultural factors).
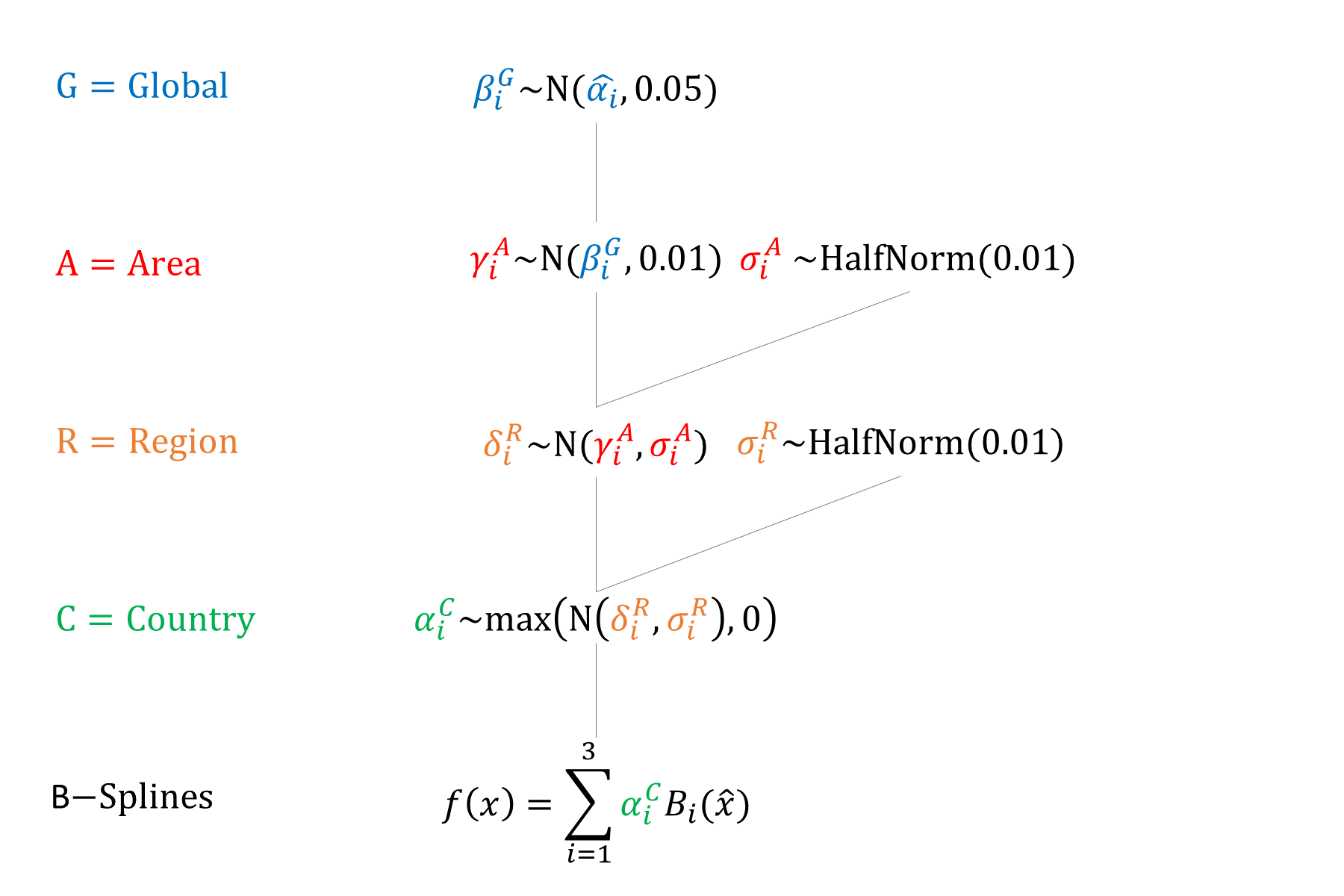
Priors
We enforced declining \(\alpha\) by age when sampling spline heights.
Model Implementation
The annual probabilities of pregnancy are converted to monthly probabilities. Age-specific natural fertility is used in the model to determine the probability of pregnancy in the absence of any contraception (or LAM).
References
- Wilson C, Oeppen J, Pardoe M. What is natural fertility? The modelling of a Concept. Popul Index 1988; 54(1): 4-20. PMID: https://www.ncbi.nlm.nih.gov/pubmed/12315189
- O’Connor KA, Holman DJ, Wood JW. Declining fecundity and ovarian ageing in natural fertility populations. Maturitas 1998; 30(2): 127-136. DOI: https://doi.org/10.1016/s0378-5122(98)00068-1
- Henry L. Some data on natural fertility. Eugen Q 1961; 8: 81-91. DOI: https://doi.org/10.1080/19485565.1961.9987465
- Coale AJ, Trussell TJ. Model Fertility Schedules: Variations in The Age Structure of Childbearing in Human Populations. Popul Index 1974; 40(2): 185-258. PMID: https://www.ncbi.nlm.nih.gov/pubmed/12333625
- Coale AJ, Trussell JT. Technical Note: Finding the Two Parameters That Specify a Model Schedule of Marital Fertility. Popul Index 1978; 44: 203-13. PMID: https://www.ncbi.nlm.nih.gov/pubmed/12337015
- Xie Y. What is natural fertility? The remodeling of a Concept. Popul Index 1990; 56(4): 656-663. PMID: https://www.ncbi.nlm.nih.gov/pubmed/12316936
- Xie Y. Model Fertility Schedules Revisited: The Log-Multiplicative Model Approach. Soc Sci Res 1991; 20: 355-368. DOI: http://dx.doi.org/10.1016/0049-089X(91)90018-X
- Xie Y, Pimental EE. Age patterns of marital fertility: revising the Coale-Trussell method. J Am Stat Assoc 1992; 87(420): 977-984. DOI: https://doi.org/10.1080/01621459.1992.10476252
- Andersen AM, Wohlfahrt J, Christens P, Olsen J, Melbye M. Maternal age and fetal loss: population based register linkage study. BMJ 2000; 320: 1708-12. DOI: https://doi.org/10.1136/bmj.320.7251.1708
- Trussell J. Contraceptive efficacy. In Hatcher RA, Trussell J, Nelson AL, Cates W, Stewart FH, Kowal D. Contraceptive Technology: Nineteenth Revised Edition. New York NY: Ardent Media, 2007. http://www.contraceptivetechnology.org/wp-content/uploads/2013/09/Contraceptive-Failure-Rates.pdf
GMatH (Global Maternal Health) Model - Last updated: 28 November 2022
© Copyright 2020-2022 Zachary J. Ward
zward@hsph.harvard.edu